


Next: Experience
Up: Hardware Techniques for Testing
Previous: Iterators
The checksum of a list of integers is the modular arithmetic sum
of the individual numbers. A single precision checksum has the
same precision P as the numbers in the list.
Checksums can be applied to permutation testing by comparing the
checksum of the elements in  to the checksum of the elements
in
to the checksum of the elements
in  .
If the checksums differ, then
.
If the checksums differ, then 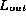 is not
a permutation of
is not
a permutation of 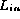 . If the checksums are the same
then
. If the checksums are the same
then 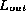 is probably a permutation of
is probably a permutation of  .
This conclusion is not always correct since the checksums
may be the same even though
.
This conclusion is not always correct since the checksums
may be the same even though 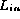 is not a permutation of
is not a permutation of  .
This situation is called error masking and the
erroneous checksum is said to be an alias of the correct checksum.
The masking characteristics associated with checksums can be measured by calculating the
proportion of all erroneous
.
This situation is called error masking and the
erroneous checksum is said to be an alias of the correct checksum.
The masking characteristics associated with checksums can be measured by calculating the
proportion of all erroneous 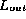 lists that cause error masking.
This is called the aliasing probability.
lists that cause error masking.
This is called the aliasing probability.
Our approach to iterator testing is as follows:
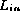 is constructed from at least one instance of each integer value in the range [0,P).
Each element of
is constructed from at least one instance of each integer value in the range [0,P).
Each element of 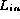 is added to
the collection class under test and the checksum for
is added to
the collection class under test and the checksum for 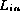 is determined.
The iterator output
is determined.
The iterator output
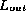 is captured and its checksum is determined.
We conclude that the iterator is fault free if
is captured and its checksum is determined.
We conclude that the iterator is fault free if
- 1.
-
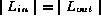
- 2.
- all elements in
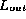 are in the range [0,P)
are in the range [0,P)
- 3.
-
 's checksum =
's checksum = 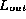 's checksum.
's checksum.
Figure 3 shows the test code required to test the iterator in IntegerSet using
a single precision checksum.

Figure 3: IntegerSet iterator test implementation
Consider an alternative approach where
each element in 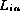 that is added to the class under test is also placed in a separate store.
Then, as each element in
that is added to the class under test is also placed in a separate store.
Then, as each element in 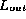 is
returned by
the iterator, it is also removed from the store. The iterator is judged fault free if the store is empty at the end of the test.
We reject this approach as too expensive;
the cost of developing and maintaining the test code and the code under test would essentially be the same.
is
returned by
the iterator, it is also removed from the store. The iterator is judged fault free if the store is empty at the end of the test.
We reject this approach as too expensive;
the cost of developing and maintaining the test code and the code under test would essentially be the same.
Saxena and McCluskey have analyzed the effectiveness of single precision
checksums used to detect errors in the storage and transmission of data [6].
They report an aliasing probability
of approximately 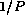 .
This result
is significant since it implies that the aliasing probability is
independent of the data and of the number of data errors.
.
This result
is significant since it implies that the aliasing probability is
independent of the data and of the number of data errors.
The analysis performed by Saxena and McCluskey is based on the assumption that all
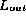 lists that contain data errors are equally likely.
This assumption
is common in the analysis of testing techniques where errors are caused by flaws in hardware [1].
The validity of this assumption is questionable in the context of iterator testing
when failures are caused by faulty programmer logic.
There is a danger that the aliasing probability is significantly higher than
lists that contain data errors are equally likely.
This assumption
is common in the analysis of testing techniques where errors are caused by flaws in hardware [1].
The validity of this assumption is questionable in the context of iterator testing
when failures are caused by faulty programmer logic.
There is a danger that the aliasing probability is significantly higher than 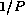 .
.
With our approach, 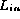 contains at least one instance of each integer in [0,P).
Previously, we gave a list of conditions we use to determine if an iterator is fault free.
The aliasing analysis need only concern itself with item 3 from this list.
Within this context, data errors in
contains at least one instance of each integer in [0,P).
Previously, we gave a list of conditions we use to determine if an iterator is fault free.
The aliasing analysis need only concern itself with item 3 from this list.
Within this context, data errors in 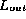 occur when
elements in
occur when
elements in  are incorrectly duplicated in
are incorrectly duplicated in 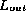 or omitted from
or omitted from  .
We assume that all elements in
.
We assume that all elements in 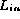 are equally likely to be
incorrectly duplicated or omitted from an erroneous
are equally likely to be
incorrectly duplicated or omitted from an erroneous  .
Consequently, it is reasonable to assume that
all flawed
.
Consequently, it is reasonable to assume that
all flawed 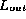 lists are equally likely resulting in an aliasing probability of at most
lists are equally likely resulting in an aliasing probability of at most 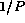 .
.



Next: Experience
Up: Hardware Techniques for Testing
Previous: Iterators
Peter Walsh
Thu Jan 18 14:37:02 PST 1996
 to the checksum of the elements
in
to the checksum of the elements
in  .
If the checksums differ, then
.
If the checksums differ, then 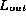 is not
a permutation of
is not
a permutation of 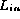 . If the checksums are the same
then
. If the checksums are the same
then 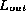 is probably a permutation of
is probably a permutation of  .
This conclusion is not always correct since the checksums
may be the same even though
.
This conclusion is not always correct since the checksums
may be the same even though 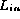 is not a permutation of
is not a permutation of  .
This situation is called error masking and the
erroneous checksum is said to be an alias of the correct checksum.
The masking characteristics associated with checksums can be measured by calculating the
proportion of all erroneous
.
This situation is called error masking and the
erroneous checksum is said to be an alias of the correct checksum.
The masking characteristics associated with checksums can be measured by calculating the
proportion of all erroneous 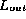 lists that cause error masking.
This is called the aliasing probability.
lists that cause error masking.
This is called the aliasing probability.
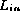 is constructed from at least one instance of each integer value in the range [0,P).
Each element of
is constructed from at least one instance of each integer value in the range [0,P).
Each element of 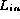 is added to
the collection class under test and the checksum for
is added to
the collection class under test and the checksum for 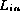 is determined.
The iterator output
is determined.
The iterator output
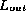 is captured and its checksum is determined.
We conclude that the iterator is fault free if
is captured and its checksum is determined.
We conclude that the iterator is fault free if
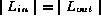
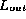 are in the range [0,P)
are in the range [0,P)
 's checksum =
's checksum = 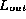 's checksum.
's checksum.

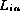 that is added to the class under test is also placed in a separate store.
Then, as each element in
that is added to the class under test is also placed in a separate store.
Then, as each element in 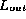 is
returned by
the iterator, it is also removed from the store. The iterator is judged fault free if the store is empty at the end of the test.
We reject this approach as too expensive;
the cost of developing and maintaining the test code and the code under test would essentially be the same.
is
returned by
the iterator, it is also removed from the store. The iterator is judged fault free if the store is empty at the end of the test.
We reject this approach as too expensive;
the cost of developing and maintaining the test code and the code under test would essentially be the same.
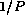 .
This result
is significant since it implies that the aliasing probability is
independent of the data and of the number of data errors.
.
This result
is significant since it implies that the aliasing probability is
independent of the data and of the number of data errors.
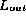 lists that contain data errors are equally likely.
This assumption
is common in the analysis of testing techniques where errors are caused by flaws in hardware [
lists that contain data errors are equally likely.
This assumption
is common in the analysis of testing techniques where errors are caused by flaws in hardware [ .
.
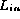 contains at least one instance of each integer in [0,P).
Previously, we gave a list of conditions we use to determine if an iterator is fault free.
The aliasing analysis need only concern itself with item 3 from this list.
Within this context, data errors in
contains at least one instance of each integer in [0,P).
Previously, we gave a list of conditions we use to determine if an iterator is fault free.
The aliasing analysis need only concern itself with item 3 from this list.
Within this context, data errors in 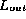 occur when
elements in
occur when
elements in  are incorrectly duplicated in
are incorrectly duplicated in 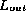 or omitted from
or omitted from  .
We assume that all elements in
.
We assume that all elements in 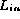 are equally likely to be
incorrectly duplicated or omitted from an erroneous
are equally likely to be
incorrectly duplicated or omitted from an erroneous  .
Consequently, it is reasonable to assume that
all flawed
.
Consequently, it is reasonable to assume that
all flawed 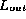 lists are equally likely resulting in an aliasing probability of at most
lists are equally likely resulting in an aliasing probability of at most 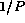 .
.